
作为deeplearn.js的继任者,tensoflow.js 支持在浏览器或者nodejs中利用JavaScript来运行深度学习。并且能够支持GPU和现有的Tensorflow的模型。该项目的首页上有几个很酷炫的演示。作为热爱机器学习和前端数据可视化的我怎能不心动呢。快来和我一起来看看如何利用tensorflow.js来进行深度学习之旅吧。
线性代数(Linear algebra)是深度学习的数学基础。张量(Tensor)是线性代数的基本数学概念和运算单元。我们来了解一下tensorflow.js中有关张量的基本概念和运算。
张量的概念
标量 Scalar
标量就是一个简单的数字,概念就是只有大小,没有方向。
const scalar = tf.scalar(5); print_tensor([scalar]);
注意:print_tensor()是我实现的一个JS方法,在浏览器中以表格的形式显示张量的内容,最高两个维度。输入是一个张量的数组。如果不想在浏览器中看到结果,也可以调用tensor.print()方法,在console中查看张量的内容。

以上的代码,创建了一个数值为5,维度(Rank)0 的标量。
向量/矢量 Vector
向量就是一个一维数组,概念就是有大小和方向。
const vector = tf.tensor1d([0, 1, 2, 3, 4]); print_tensor([vector]);

以上的代码,创建了一个数值为[0,1,2,3,4],维度 1 的向量。形状(Shape)描述了各个维度的容量或者说大小,这里是5.
张量 Tensor
矩阵(Matrix)拥有两个维度,在更高的维度,就是张量。其实所有的标量,矢量,矩阵都可以用张量表示,只是维度不同。
在Tensoflow中Rank表示了维度的等级,对应如下
- 标量 0 tf.scalar
- 矢量 1 tf.tensor1d
- 矩阵 2 tf.tensor2d
- 张量 2+ tf.tensor3d, tf.tensor4d
const matrix = tf.tensor2d([[1.0, 2.0, 3.0], [10.0, 20.0, 30.0]]); print_tensor([matrix]);

以上的代码,创建了一个数值为[[1.0, 2.0, 3.0], [10.0, 20.0, 30.0]],维度 2 的矩阵。形状是2X3,两行,三列。
一张图来直观说明:
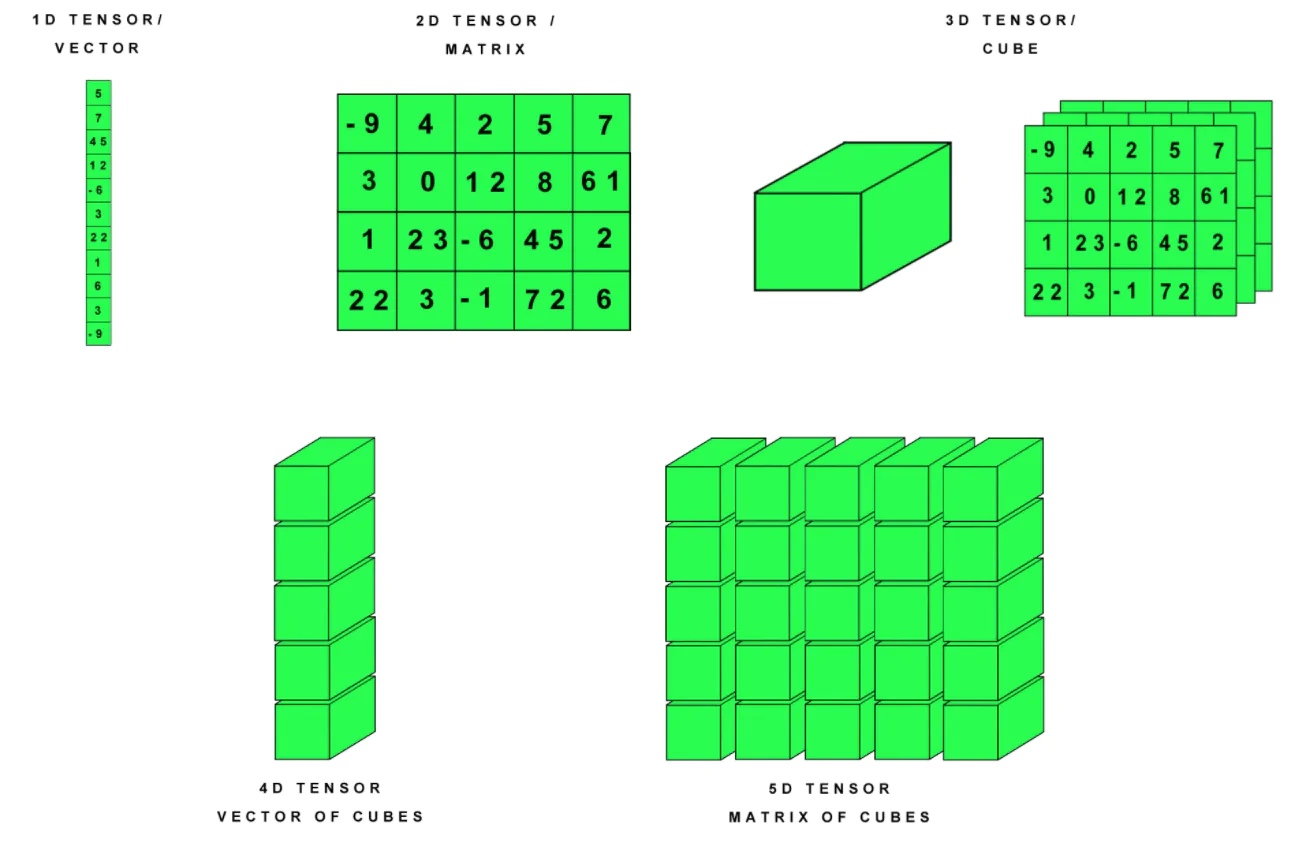
tensorflow.js提供了对张量的创建和生成,变形,切片和合并等方法,用于对数据的准备。
张量的运算
张量-标量运算
张量和标量之间的数学运算(加减乘除幂)比较简单,只要直接把张量的每一个元素和标量进行对应的数学运算就好了。
const t = tf.tensor([[1.0, 2.0, 3.0], [10.0, 20.0, 30.0]]); const s = tf.scalar(3); print_tensor([t,s,t.add(s),t.mul(s)])
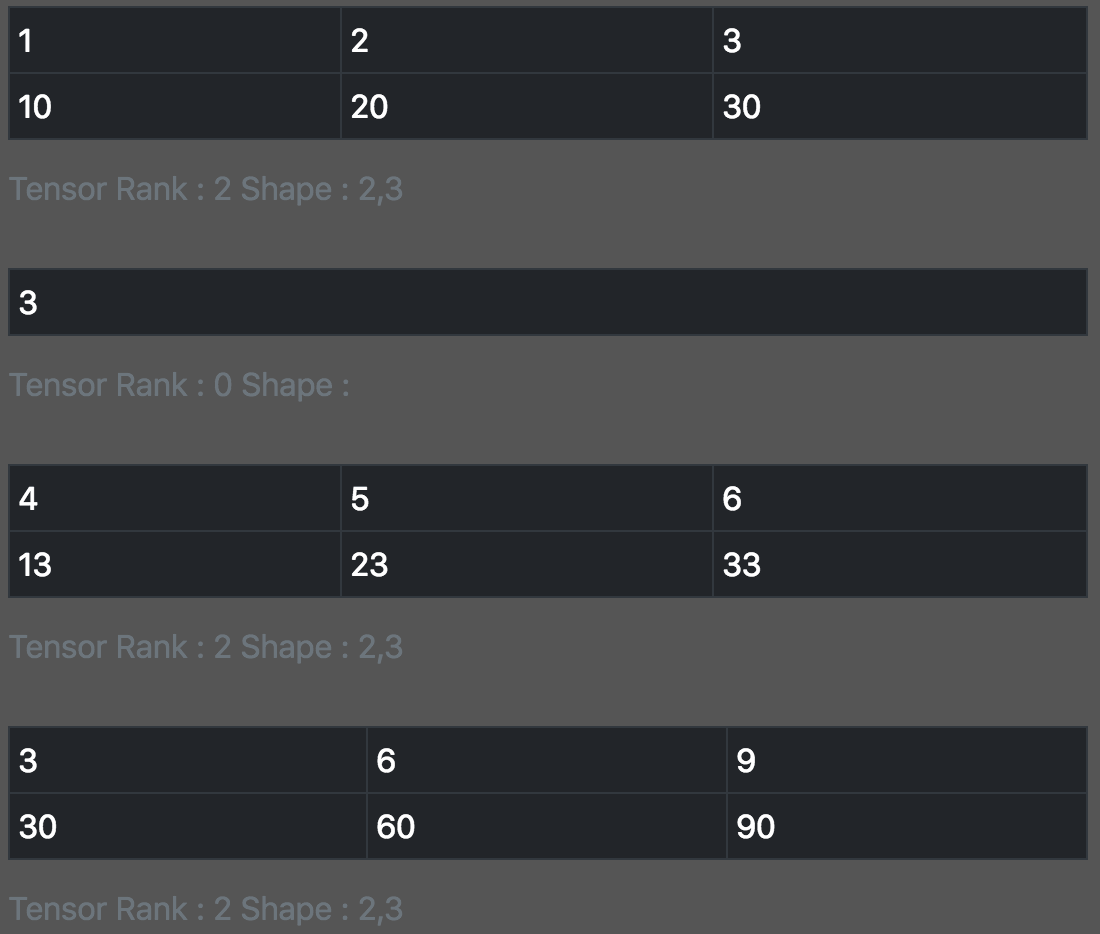
张量和标量的数学运算不会改变张量的形状,并且满足算术运算的基本定律,例如加法交换律,乘法结合律等等。
张量-张量加减乘
具有相同形状的张量可以进行加减操作。只要把对应的元素做加减就好了。
const a = tf.tensor1d([1, 2, 3, 4]); const b = tf.tensor1d([10, 20, 30, 40]); print_tensor([a,b,a.add(b),a.sub(b),a.mul(b)])
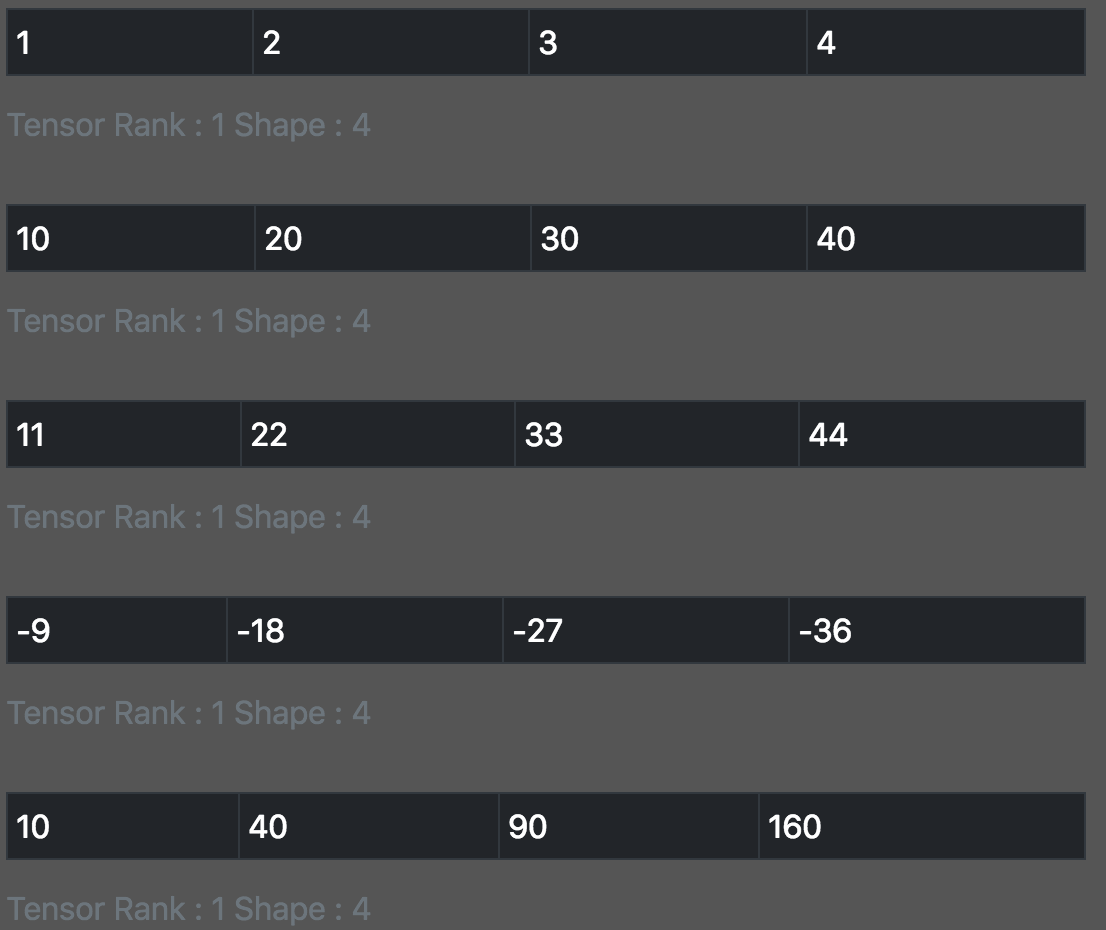
张量-张量 点积
张量的积 tensor.matMul() 在深度学习中被大量的应用,下图给出了一个矩阵点积的例子:
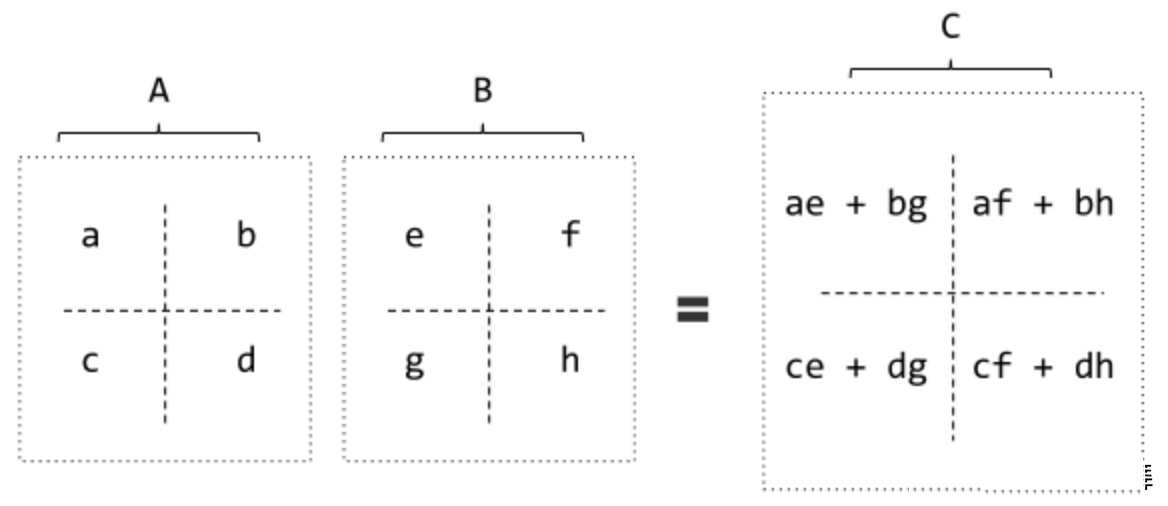
简单说一个m*n的矩阵和一个n*k的矩阵的点积得到一个m*k的矩阵。
const a = tf.tensor2d([[1, 2], [3, 4]]); const b = tf.tensor2d([[5, 6, 7], [7, 8, 9]]); print_tensor([a, b, a.matMul(b)]);
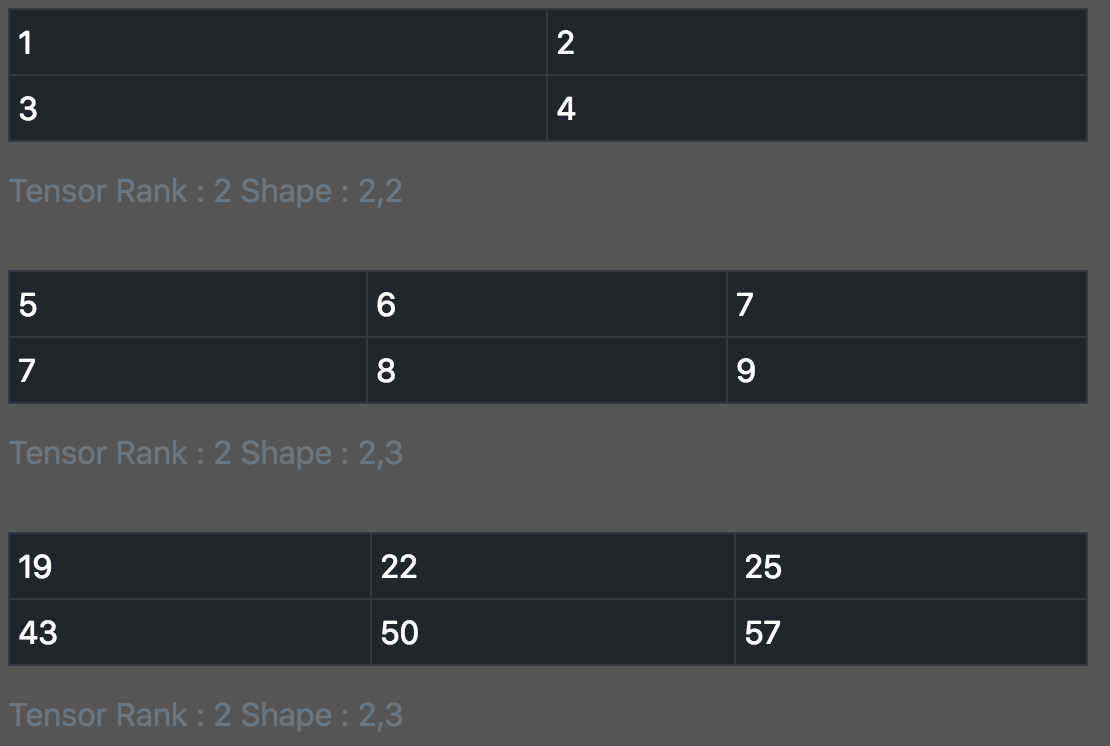
注意,矩阵的点积不满足乘法交换律,AB != BA
const a = tf.tensor2d([[1, 2], [3, 4]]); const b = tf.tensor2d([[5, 6], [7, 8]]); print_tensor([a, b, a.matMul(b), b.matMul(a)]);
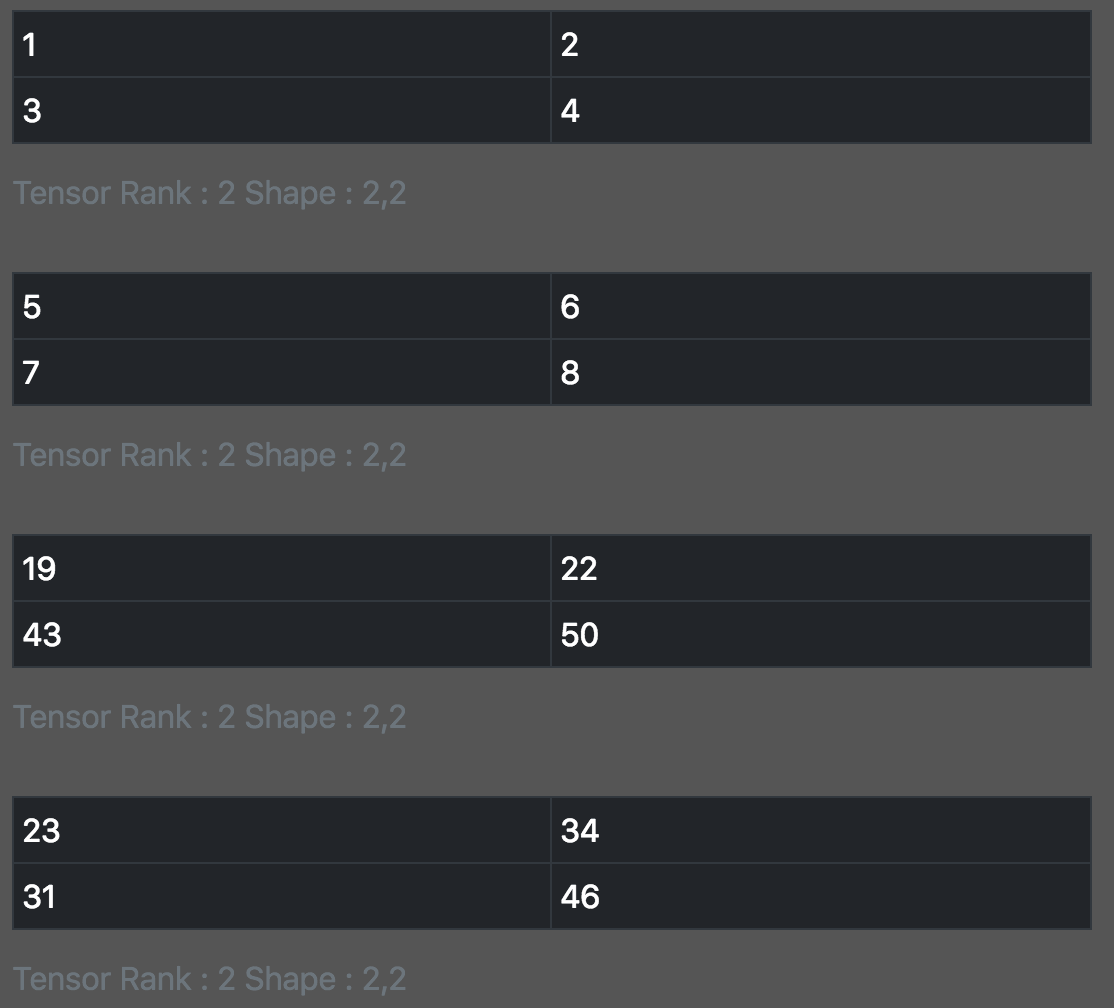
矩阵转置 (Transpose)
矩阵的转置就是将矩阵的所有元素绕着一条从第1行第1列元素出发的右下方45度的射线作镜面反转,即得到矩阵的转置。
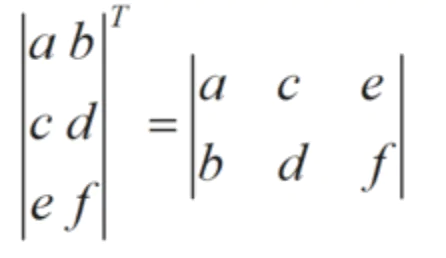
const a = tf.tensor2d([[1, 2], [3, 4],[5,6]]); print_tensor([a, a.transpose()]);
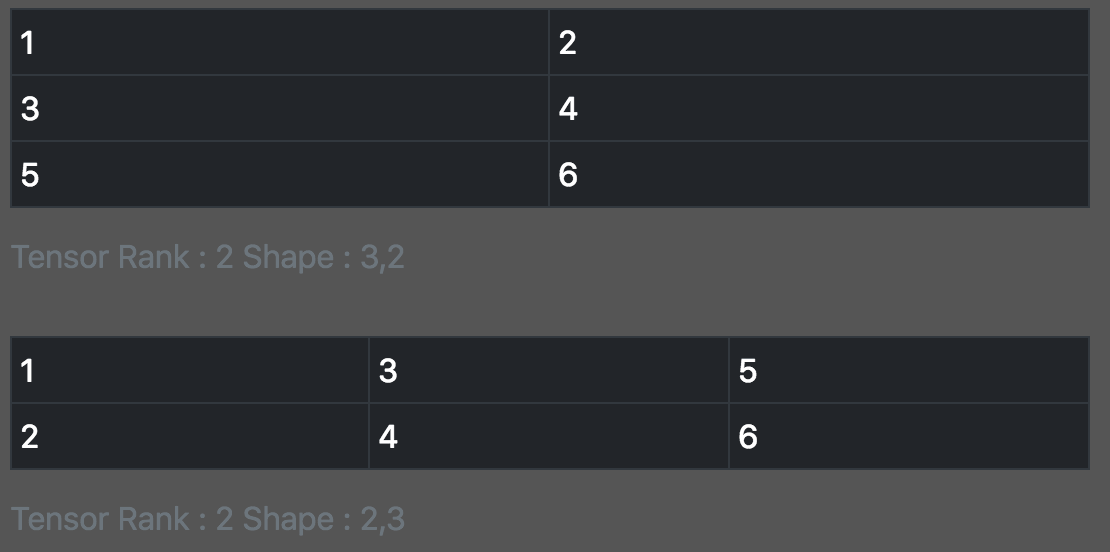
单位矩阵(Identity Matrix)
就像数学中的1,任何数字和1相乘都是这个数本身。单位矩阵的特性就是任何矩阵和单位矩阵的点积的结果都是原矩阵本身。单位矩阵就是一个n*n的矩阵对角线上的元素都是1,其它为0。
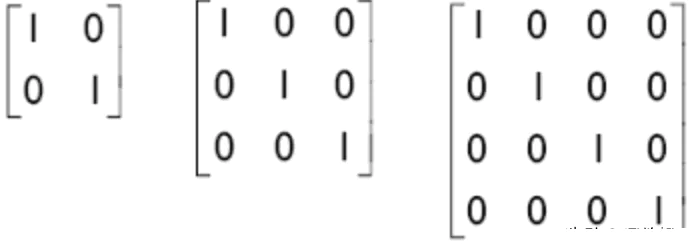
利用tf.oneHot() 可以生成一个单位矩阵。
const identity = tf.oneHot(tf.tensor1d([0, 1, 2]), 3); print_tensor([identity]);
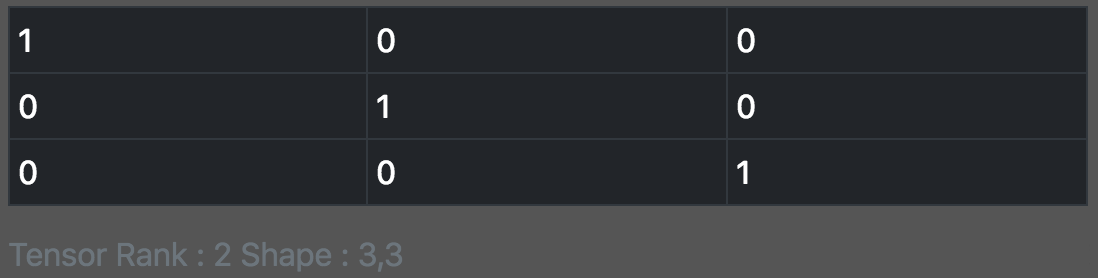
我们以后再去研究利用tf.initializers.identity来初始化单位矩阵。
矩阵的逆 (Inverse)
如果一个矩阵和另一矩阵相乘得到单位矩阵,那么这个矩阵就是该矩阵的逆。
tensorflow 提供了矩阵的逆操作,tf.matrix_inverse
然而tensorflow.js中并没有对应的操作。(考虑到当前的版本是0.6.1,我们就忍了。另外据说深度学习并没有用到任何矩阵的逆操作。)
注意,并不是所有的矩阵都是可逆的,有些矩阵找不到逆矩阵。
进一步了解矩阵的逆可以参考这篇文章
两个矩阵的除法可以理解为一个矩阵和另一个矩阵的逆的点积。
Reduction
深度学习中常常需要对张量各个维度进行统计。例如求均值,总和等等。tensorflow.js提供了相应的操作。
const x = tf.tensor2d([[1, 2, 3],[4,5,6]]); print_tensor([x, x.mean(),x.max(),x.min(), x.sum()]);
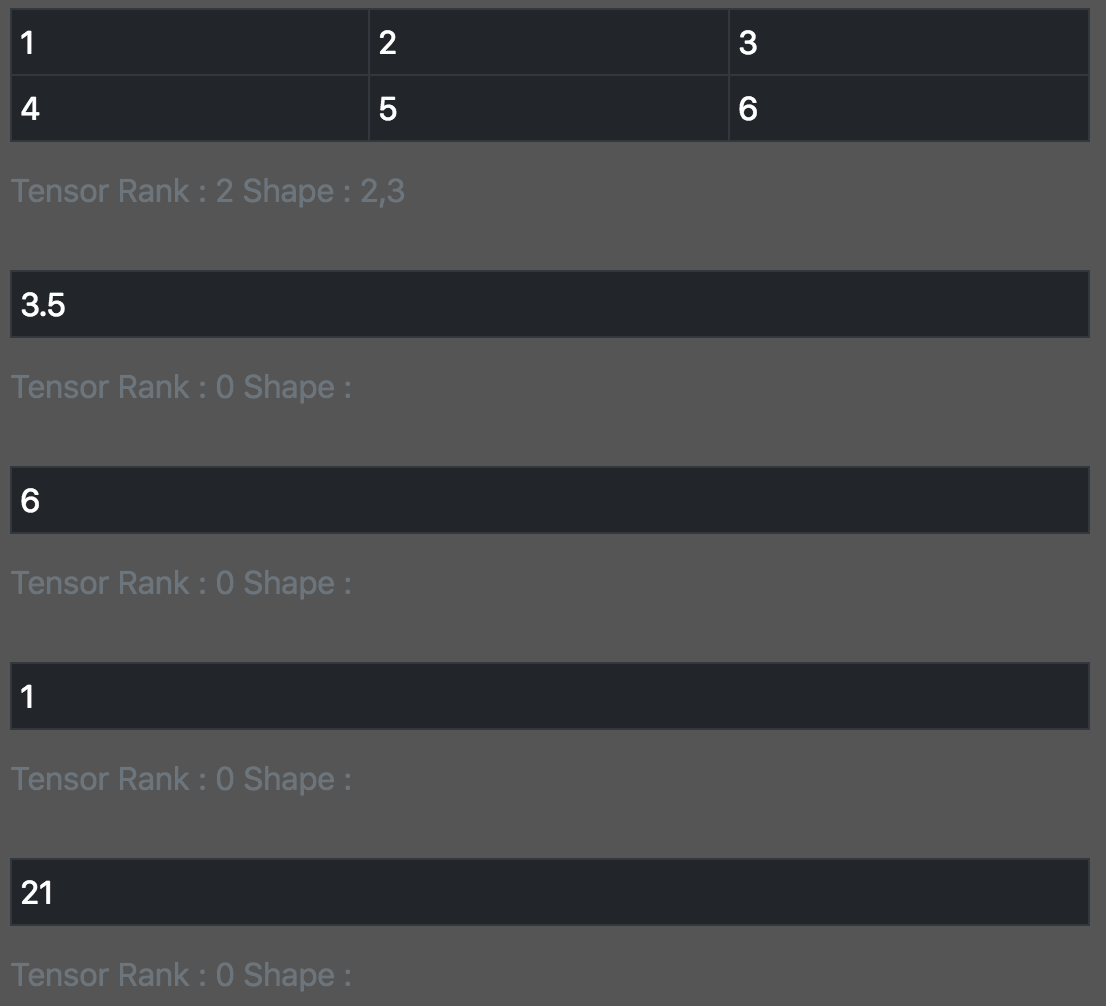
这里给出了一个矩阵的所有元素的均值,最大值,最小值和总和,也可以针对行和列做相应的操作。
下面的代码对于每一列做相应的统计。
const x = tf.tensor2d([[1, 2, 3],[4,5,6]]); print_tensor([x, x.mean(0),x.max(0),x.min(0), x.sum(0)]);
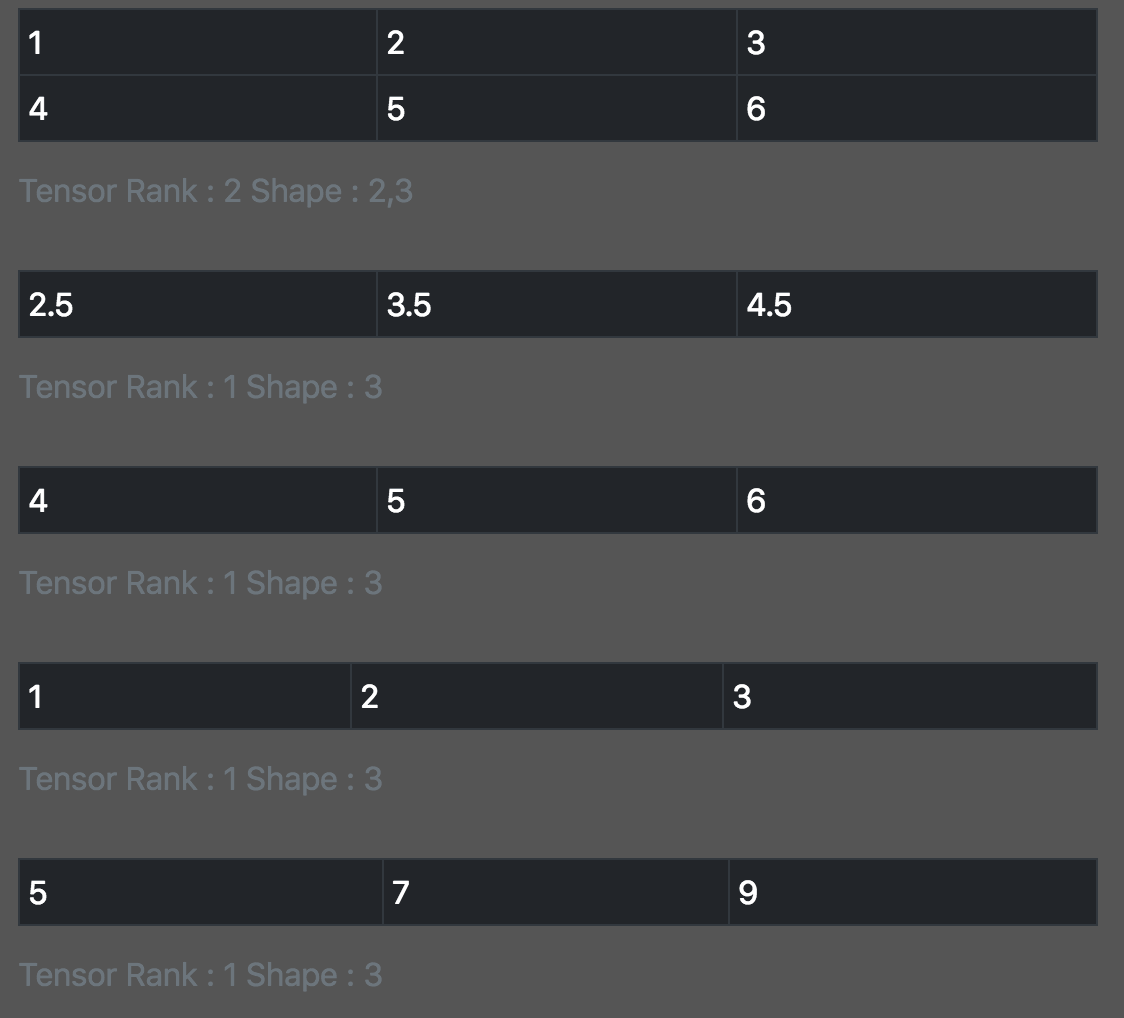
除了上面提到的操作,tensorflow.js还提供了:
- 基本的数学运算诸如三角函数,对数,开方等
- 逻辑操作
- … …
总结
本文描述了张量的基本概念和操作,并给出了tensorflow.js中的代码例子。线性代数作为机器学习,尤其是深度学习的数学基础,值得大家去了解和掌握。
